A Computational Model of Some Key Socially Significant Processes

Received: 01-Dec-2022, Manuscript No. CSRP-22-76831; Editor assigned: 05-Dec-2022, Pre QC No. CSRP-22-76831(PQ); Reviewed: 22-Dec-2022, QC No. CSRP-22-76831; Revised: 29-Dec-2022, Manuscript No. CSRP-22-76831(R); Published: 06-Jan-2023, DOI: 10.3371/CSRP.FVAA.010623

Introduction

Medicine, and especially some of its areas, such as cardiology, neurology and oncology [1], most urgently needs adequate simulation and mathematical models at all levels of living matter organization [2], from the cellular to population ones. For natural reasons, there are a number of difficulties in conducting in vivo experiments on wildlife and, especially, on humans [3]. That is why structural, functional, simulation models in Silico are so relevant. Noteworthy, there are still no simulation mathematical models to operate with the ischemic brain stroke pathogenesis scenaria [4].

Stroke is the second largest death reason in the world according to WHO data [5], which is why research in the field of finding effective drugs for the treatment of this disease is of particular relevance. The development and introduction into circulation of pharmaceuticals is a complex and lengthy process that requires extensive preclinical and clinical studies. That is why the optimization of such scenarios by means of mathematical modeling using information and computer technologies is a separate extremely important task of a scientific and practical nature.

Stroke is the world's second leading cause of death, accounting for approximately 6,000,000 deaths each year. The lifetime risk of stroke is estimated to be between 8% and 10%. Stroke pathogenesis involves a diverse set of processes. Vessel occlusions (ischemic stroke) account for 85% of all strokes, with the remainder caused by primary intracerebral bleeding (hemorrhagic stroke). Embolisms are the most common cause of focally obstructed blood flow within the brain, accounting for approximately 75% of all cerebral vessel occlusions. Ischemia is defined as a decrease in blood flow severe enough to disrupt normal cellular function. Ischemia is so sensitive to brain tissue that even brief ischemic periods in neurons can set off a complex chain of events that can lead to cellular death.

The solution of this problem is possible in silico in the paradigm of a computational experiment. In this case, it is necessary to model not only the pharmacokinetics (i.e., the delivery of the drug to the selected organ), but also the pharmacodynamics or, in other words, the therapeutic effect of its impact on the course of the disease under study [6]. And this means that in addition to the model of the disease itself (in our case, stroke), it is necessary to have a model of the pharmacokinetics of the study drug and a model of its pharmacodynamic effects.

Research is complicated not only by the lack of relevant descriptions of mathematical models of ischemic stroke in the literature, but also by the lack of pharmacokinetic models of innovative drugs under investigation, the pharmacokinetics of which can have a pronounced drug-specific character, especially when it comes to targeted delivery. At the same time, the rapidly developing branch of nanopharmacology offers a number of innovative drugs of the nano-group, the pharmacokinetics of which are fundamentally different from traditional drugs, but at the same time, the prospects for using them as neuroprotectors can hardly be overestimated [7].

Methodology

Here we present a two-dimensional discrete stochastic model developed by us for the evolution of elementary states of neurovascular units in the area of cerebral ischemia in stroke after occlusion of a small arteriole. This is a lattice model with a unit cell, which is a morph functional element of the brain tissue-a neurovascular unit.

Mathematical models of biological systems are usually divided into homogeneous and heterogeneous models (in their stationary or dynamic variants), and these models are obtained mainly within the framework of the following generally accepted approaches.

The first approach is to average variables over space and consider the system as homogeneous. Such models are called kinetic. Mathematically, they represent a set of systems of Ordinary Differential Equations (ODEs) with respect to the averaged values of the variables under study. In particular, in the works of Dronne, et al. presented a kinetic model of the behavior of brain cells under conditions of stroke [8]. The model well described the change in the state of cells in the epicenter of the affected area, under conditions of reduced blood flow. However, biomedical interest is not limited to these cells. It is also important to describe the spatial development of the lesion to neighboring areas, including those in which the blood flow is not disturbed. It is often necessary to determine the spatial characteristics of the affected area, and in this case kinetic models are not informative enough.

The second approach is applicable directly to heterogeneous models. In it, the dynamics of the system variables is described by a set of partial differential equations with boundary and initial conditions. Such equations are usually solved numerically using methods based on finite-difference approximations of partial differential equations. So, in the work of Chapuisat, et al. considered a finite-difference model of stroke development. At the same time, the general disadvantages of finite-difference models are their general complexity and complexity of setting boundary conditions, supplemented also by the fact that the cerebral cortex has a complex shape and consists of heterogeneous elements [8].

The third approach is based on the discretization of the system and the transition from variables describing concentrations to individual discrete elements. The methods used in such simulations include Monte Carlo methods [9], molecular dynamics methods, particle methods, etc. Currently, there are no discrete models for the development of ischemic stroke. The advantage of discrete models is the convenience of their implementation in the form of parallel programs, sufficient ease of implementation, good convergence. However, a large total number of elements can nevertheless make such models laborious.

Thus, in this field of science, it is important to create new adequate mathematical models that contain a relatively small number of parameters and variables and are easy to implement numerically [10].

Within the framework of our hypothesis, the elementary unit of the model might exist in one of the elementary states namely in physiological, ischemic, or destruction (implying apoptosis or necrosis) ones. Once ischemia is in the case, each cell of the lattice, as well as the neighbouring cells can change its state with a given transition rate. The possibility of transition to another state for each particular cell obeys a stochastic law which makes it treatable by the Monte Carlo method [4,11]. The model is implemented as a computer program driven in the Python 3.9 language which allows to run the parallel calculations to simulate the development of a stroke under various conditions.

Results and Discussion

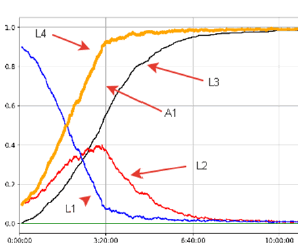
On a 30 × 30 grid of 900 neurovascular units, we have modeled the development of a “Perfect Stroke” in case of occlusion of a small arteriole, which is a section of a brain tissue area with a side of about 3 mm [12]. Figure 1 shows the visualization of data on changes in the structure of this section as a function of time.

Figure 1.Transition of the states of simulated areas. On the abscissa axis-the fractional content of neurovascular units in each of the elementary states in relation to their total number. On the y-axis-time in the format "hours: minutes: seconds”.

On the graph, one can observe the growth of the L4 curve, which reflects the growth of the total number of damaged neurovascular units. This curve is cumulative with respect to the L3 curve (the number of neurovascular units subjected to destruction) and the L2 curve (Ischemic Neurovascular Units). Line L1 reflects the content of undamaged lattice sites. Area A1, bounded by the lines L4 and L3, reflects the presence of a “Therapeutic Window”, which, during morphological examination, is found as a penumbra around the core of the destruction of the ischemic area [14]. After the mark of 400 minutes (3 hours 20 minutes), there is a steady decrease in viable morph functional units (L1 and L2) with complete disappearance at around 600 minutes (10 hours). At the same time, 50% of the damaged cells of the studied area are formed by the hundredth minute from the onset of ischemia. The data obtained correlate well with published studies on the morphology of stroke development using biological models [12,13].

Conclusion

Thus, the model we developed can be used to study the influence of various conditions on the development of cerebral stroke. As a result of the study of the model under the conditions of the “Ideal” development of stroke, we obtained data that are significantly correlated with the clinical data published in the literature. By setting the appropriate parameters, the model can be used to study and predict the impact of external influences on the development of stroke, such as the administration of drugs, changes in the composition of the inhaled air, and changes in the composition of the blood.

Funding

The work was supported by the grant of the Ministry of Science and Higher Education of the Russian Federation No. 075-15-2020-792 (Unique identifier RF----190220X0031).

Conflict of Interest

The Authors declare no Competing Financial or Non-Financial Interests. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Author Contributions

Dr. V.V. Fursov – general project management, experiment planning, In Silico research management, idea, hypothesis, structure, modeling, text; Mr. Aleksandr V. Ananyev – modeling, program code, text; Ryabov, V., Ananishnev, V., Tkachenko, A., Osmolovskaya, S., Frolova, T., Berestova L. – analysis and discussion of the data obtained

References

1. RJ, Johansen, Bukhvostov AA, Ermakov KV, and Kuznetsov DA. "Towards a Computational Prediction for the Tumor Selective Accumulation of Paramagnetic Nanoparticles in Retinoblastoma Cells." Russ. State Med. Univ 6(2018): 68-73.

   [Google Scholar] [Crossref]

2. Fursov, Valentin V, Ilia V. Fursov, Alexander A. Bukhvostov and Aleksander G. Majouga, et al. "In Silico Studies on Pharmacokinetics and Neuroprotective Potential of 25 Mg2+: Releasing Nanocationites- Background and Perspectives." Pharmacogenetics (2021): 155.

   [Google Scholar]

3. Buryak, AA, AV Dudko, EA Laneeva. The use of Computer Modeling in Medicine. Problems and Prospects for the Introduction of Innovative Telecommunication Technologies: Collection of Materials of the VII International Scientific and Practical Part time Conference, Orenburg. 2021: 200-204.
4. Zhuykova, AA. "Application of Simulation Modeling in Medicine." Forum of Young Scientists 32(2019): 356-358.
5. "Global health estimates: Leading causes of death." World Health Organization.
6. Fursov, Ivan V, DI Zinchenko, VV Fursov and VM Ananishnev. "Artificial Intelligence Technologies in Health Care. Development of in Silico Algorithms for Optimization in Experimental Nanopharmacology of Ischemic Stroke. Collection of Works of Teachers, Graduate Students and Students." Moscow: Pero Publishing House. 2022: 30-33.
7. Salmina, Alla Borisovna, NA Malinovskaya, NV Kuvacheva and AV Morgun, et al. "Connexin and Pannexin Transport Systems in the Cells of the Brain Neurovascular Unit."Neyrochimia-Neurochem J 31(2014): 122-133.

   [Google Scholar] [Crossref]

8. Chapuisat, Guillemette, Marie-Aimée Dronne, Emmanuel Grenier and Marc Hommel, et al. "A Global Phenomenological Model of Ischemic Stroke with Stress on Spreading Depressions." Prog Biophys Mol Biol 97(2008): 4-27.

   [Google Scholar] [Crossref]

9. Krausch, Niels, Tilman Barz, Annina Sawatzki and Mathis Gruber, et al. "Monte Carlo Simulations for the Analysis of Non-Linear Parameter Confidence Intervals in Optimal Experimental Design."Front Bioeng Biotechnol 7(2019): 122.

   [Google Scholar] [Crossref]

10. Ananishnev, Vladimir Maksimovich, VV Ryabov, AV Tkachenko and SM Osmolovskaya, et al. "Monitoring a University's Educational and Scientific Activities: Unifying the Monitoring Processes with European International Standards." Int. J. Innov. Creativity Chang 11(2020): 56-69.

    [Google Scholar]

11. Dronne, Marie-Aimee, Jean-Pierre Boissel, and Emmanuel Grenier. "A Mathematical Model of Ion Movements in Grey Matter During A Stroke." J Theor Biol 240(2006): 599-615.

    [Google Scholar] [Crossref]

12. Kiryanova VV, Molodovskaya NV, Zharova EN. "Morphological Aspects of the use of Transcranial Methods of Physiotherapy in the Early Period of Ischemic Stroke." Bulletin of Physiotherapy and Balneology 2(2019): 34-40.
13. Korneva, Yulia, and Alexander Dorosevich. "Dynamic of Morphological Changes in Border Zone During Myocardial Infarction Organization."

    [Google Scholar] [Crossref]

Citation: Fursov, Valentin V, Aleksandr V. Ananyev, Vladimir M. Ananishnev and Alexander V. Tkachenko, et al. "A Computational Model of Some Key Socially Significant Processes.” Clin Schizophr Relat Psychoses 16S (2023). Doi: 10.3371/CSRP.FVAA.010623

Copyright: © 2023 Fursov VV, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.